 Separata de la revista El Catoblepas • ISSN 1579-3974
Separata de la revista El Catoblepas • ISSN 1579-3974
publicada por Nódulo Materialista • nodulo.org
 Separata de la revista El Catoblepas • ISSN 1579-3974
Separata de la revista El Catoblepas • ISSN 1579-3974
publicada por Nódulo Materialista • nodulo.org

El Catoblepas • número 88 • junio 2009 • página 2
Sumario
Introducción. Presupuestos sobre instituciones
I. Distinción entre instituciones holomórficas e instituciones meromórficas
II. Sobre la estructura noetológica del teorema I,1 de Euclides
III. Sobre la estructura noetológica del soneto CLXXXVIII de Lope de Vega
Final. Poesía y Verdad [en el próximo número de El Catoblepas]


Introducción
1. El día 27 de mayo próximo pasado se celebró en Oviedo, en la Fundación Gustavo Bueno, una jornada dedicada a analizar y debatir el ambicioso proyecto, rotulado con ciertos ecos kantianos («en torno a una crítica de la razón literaria»), del profesor Jesús G. Maestro, que va tomando cuerpo desde hace seis años, y que gira en torno a las relaciones entre la Literatura y la Ciencia, por un lado, y entre la Teoría gnoseológica de la ciencia y la Teoría de la Literatura, por otro. Una excelente reseña más amplia de las tres sesiones de esta jornada (cuya grabación en video está publicada en las páginas de la Fundación), realizada por su coordinador, Marcelino Suárez Ardura, aparece publicada en este mismo número de El Catoblepas –«Materialismo Filosófico y Literatura»– y a ella me remito.
En el curso de una de aquellas sesiones salió a relucir incidentalmente un ensayo mío de hace algunos años, inédito, en el cual, y a vueltas del proyecto de Noetología (véase El Catoblepas, nº 1, marzo 2002), se exploraban ciertos paralelismos entre algunos «poemas argumentativos» (entendiendo por tales aquellos poemas que tratan, al parecer, de «demostrar» algo, como pudiera serlo el célebre soneto de Lope de Vega, «Suelta mi manso, mayoral extraño», que en adelante denominaremos como «soneto canónico») y algunas proposiciones de Euclides, ordinariamente clasificadas en dos tipos, los llamados «problemas» y los llamados «teoremas», que se reconocen, como es sabido, porque en su exposición terminan con la fórmula ὅπερ ἔδει ποιῆσαι, es decir, «como había que hacer», a diferencia de las proposiciones del segundo tipo, los «teoremas», que terminan con la fórmula ὅπερ ἔδει δεῖξαι, es decir, «como había que demostrar» (Quod erat demostrandum, Q. E. D.). En este rasguño reexponemos aquel ensayo inédito.
2. Obviamente, la afinidad constatada entre algunos sonetos (en cuanto poemas) y algunos teoremas de Euclides (en su sentido amplio, que incluye también a los problemas), no se fundamenta únicamente en la «marca» citada para los «teoremas poéticos» (ὅπερ ἔδει ποιῆσαι), sino también en paralelismos de circunstancias consideradas a veces como externas (extralingüísticas), pero que nosotros, desde la teoría de las instituciones que presuponemos (ver El Basilisco, nº 37, julio-diciembre 2005), consideramos como circunstancias esenciales de contexto histórico-institucional, a saber, la estructura artificiosa tanto de los teoremas (cuyo curso suele disponerse en torno a las catorce líneas) como de los sonetos (cuyos versos también se suceden en número de catorce). Una estructura artificiosa cuya creación, y sobre todo, su consolidación sólo podría explicarse en función de una «aristocracia», es decir, no de una sociedad popular o plebeya, ni siquiera «burguesa», en la que pudiesen haber cristalizado tanto la forma de los teoremas de Euclides como la de los sonetos de Giacomo da Lentino: el contexto de una corte imperial como pudiera serlo la del emperador Tolomeo de Alejandría (304-285 antes de Cristo), en el caso de Euclides, y la corte imperial del emperador Federico II Hohenstaufen (que reinó en Sicilia y Nápoles durante los años 1208 y 1250).
Es muy conocida la anécdota, que podemos leer en el llamado Sumario de Proclo, según la cual cuando Euclides presentó a Tolomeo los Elementos, cuya redacción él mismo le había pedido, le preguntó si no había un camino más corto para aprender Geometría que el de los Elementos que le había entregado. Euclides habría contestado: «No hay caminos reales a la Geometría» (μή είναι βασιλικήν άτραπόν έπί γεωμετρίαν). Esta célebre respuesta, interpretada desde la perspectiva de un «demócrata republicano» podría entenderse como la reivindicación que un «plebeyo», un meteco, como Euclides, formuló al Rey: «El Rey, si quiere saber Geometría, tiene que seguir el mismo duro camino que los demás mortales». Pero interpretada en un contexto histórico constituye una crítica radical a las pretensiones de las democracias «realmente existentes», las que conceden a cualquier ciudadano el derecho a opinar en pie de igualdad, y sin esfuerzos previos, sobre cualquier asunto, y rechazar, como elitista, todo aquello que implica un esfuerzo. El sentido de la respuesta de Euclides podría interpretarse también de este modo: «Es preciso que tú, oh rey, sepas que la Geometría requiere esfuerzos que en modo alguno pueden serte evitados, y en consecuencia debes saber que si es preciso que tus súbditos, bajo tu patrocinio, aprendan Geometría y sepan que aquí no cabe ‘opinar libremente’, será necesario educarles con rigor, sin ceder a las simplificaciones demagógicas a las que la plebe perezosa, alentada por los demagogos, tiende.»
Dicho de otro modo: Euclides, en la corte imperial, y al tanto de su grandeza y poder, se identifica con ella, y se atreve a proponer unas instituciones artificiosas (los teoremas) que a la plebe pueden parecer ociosos y superfluos, pero que son necesarios; y, al mismo tiempo, el rey advierte que al proteger al geómetra sigue su objetivo de mantener el prestigio aristocrático en un terreno en el cual puede tener acceso el pueblo, pero siempre que se esfuerce en la disciplina impuesta por la aristocracia.
En suma, mediante estas instituciones artificiosas, tan distantes de las groseras aproximaciones a los teoremas geométricos de los albañiles o de los carpinteros, la aristocracia apoya a los verdaderos artistas (a las futuras artes liberales, del también futuro quadrivium), a la vez que, a través de la disciplina en esas artes, mantiene la jerarquía entre la aristocracia y el pueblo, puesto que sabe que la élite, sólo amparada por el poder, puede mantener sus distancias con la plebe. De modo parecido cabrá, en lo sucesivo, distinguir la música trivial (la que se llamará «música pop» y afines) de la música cuadrivial (escolástica, académica...), que hoy ya no podríamos llamar «clásica» (desde el momento en el cual también hablamos, en el terreno del trivium, de los «clásicos del pop»).
En cualquier caso, las instituciones euclidianas (los teoremas y problemas de sus Elementos) constituirán, en adelante, un canon de racionalidad, y no sólo de la racionalidad geométrica en general, sino de la racionalidad geométrica axiomática y jerárquica. Todavía D. Hilbert subrayaba la involucración entre la Geometría y la jerarquía de una sociedad política fuerte –que los «nuevos filósofos franceses» se atrevieron a llamar «fascista»–: «los Estados... tienen un virtual deseo de que reine el orden, no sólo en su interior, sino en sus mutuas relaciones. Lo mismo ocurre en la vida de las ciencias...» (remitimos a TCC, I, pág. 287).
Casualmente además, como ya hemos dicho, los teoremas de Euclides se despliegan, en general, precisamente a lo largo de aproximadamente catorce líneas, a su vez reclasificadas según diferentes criterios (el más importante, y al que nos atendremos en adelante, el de las seis fases propuestas por Proclo: (1) Prótasis, (2) Ekthesis, (3) Diorismós, (4) Kataskeué, (5) Apódeixis, y (6) Sympérasma). Fasificación cuyos fundamentos son muy confusos, y precisamente por ello, requieren una refasificación. El mismo Proclo propuso una refasificación ternaria –enunciado / demostración / conclusión– que, como es fácil ver, resulta ser excesivamente ambigua y externa. Más adelante propondremos una refasificación también ternaria, pero inspirada en criterios noetológicos.
Pero es importante retener el hecho de que los teoremas euclidianos suelen desarrollarse en catorce líneas, en la mayor parte de las publicaciones, tales como la traducción española, publicada por la UNAM en 1944, de García Bacca (que sigue, por otra parte, la edición teubneriana de Euclides a cargo de J. Heiberg y H. Menge, Euclidis opera omnia, Leipzig 1883, libro primero). Y estas aproximadamente catorce líneas o pasos se reproducen en las proposiciones sucesivas de los Elementos, tanto si son problemas como si son teoremas. También es verdad que esta sucesión en «catorce líneas» queda enmascarada cuando se utiliza la numeración bifurcada (que Wittgenstein utilizó en su Tractatus) –del tipo (1.1), (1.2), (1.3.1), (1.3.2)–, y este enmascaramiento explicaría el que no aparezca ninguna mención, aún a título de «curiosa coincidencia», entre las catorce líneas que en general tienen los teoremas euclidianos, y los catorce versos que «dicen que es soneto».
Por supuesto, ni los pasos de este canon, ni sus fases, surgieron de una vez en la obra de Euclides. Por ejemplo, el diorismós (según nos informa el propio Proclo en el lugar citado) habría sido descubierto por León, discípulo de Neoclides: los diorismós establecen aquellas condiciones según las cuales el problema investigado podría ser resuelto, y aquellas condiciones en las cuales no puede serlo. Es famoso el diorismós al que alude Platón en Menon 86e-87b, relativo a la inscripción de un área rectangular X=AF.FE=b2 en la forma de un triángulo, en un círculo (AF es un lado del triángulo rectángulo AFE, inscrito en la circunferencia de centro O y diámetro AB; E es un punto perteneciente a una hipérbola rectangular de la cual AB y AC son asíntotas). Para que la solución sea posible –y en el análisis de esta posibilidad consiste el diorismós– es preciso que b2 no sea mayor que el triángulo equilátero inscrito en el círculo, es decir, no sea mayor que 3√3.a2/4, siendo a el radio del círculo; si b2 es igual a esta área –dice el diorismós– la hipérbola toca al círculo, y hace posible la única solución; si b2 es mayor que esta área la hipérbola no lo toca, y no cabe solución al problema; y si b2 es menor que el área, la hipérbola corta al círculo en dos puntos E, E’ y da dos soluciones posibles.
Asimismo, la demostración del más importante teorema del libro primero de Euclides, el teorema 47 (llamado «teorema de Pitágoras»), que también se desarrolla a lo largo de catorce líneas, numeradas en algunas ediciones, no fue, desde luego, el único camino que fuera necesario recorrer; sin contar las «demostraciones estéticas» (llamadas también «intuitivas»), para el caso de encajes de triángulos rectángulos isósceles, el teorema podría ser demostrado de una manera mucho más sencilla, mediante un silogismo de sustitución, contando con el «punto de Herón» que Euclides no cita en su demostración; pero en cambio, partiendo de la teoría de las proporciones expuesta en el libro VI, y dado el triángulo rectángulo ABΓ y las proyecciones AM (en BΓ de AB y AΓ) podríamos escribir el siguiente «silogismo»:
BA2 = BM. BΓ
AΓ2 = ΓM. BΓ
BA2 + AΓ2 = BΓ2 [= BΓ.(BM + ΓM)]
3. Se ha sugerido que Euclides habría podido probar su teorema más famoso (el de Pitágoras) a partir de su doctrina de las proporciones, aplicada únicamente a las magnitudes conmensurables; pero que sólo cuando se descubrieron los inconmensurables, se habría hecho necesaria una nueva prueba, como la de Euclides I,47, independiente de la teoría de las proporciones (vid. Ivor Thomas, Greek Mathematics, vol. I, Harvard University Press, 1980, pág. 181).
En cualquier caso, es obvio que a la «coincidencia» entre el número catorce (aproximado) de los pasos de los teoremas de Euclides y el de los versos del soneto no cabe darle ningún fundamento cabalístico o aritmológico, por no decir mágico. Pero no por ello esta coincidencia carece de significado estructural –que más adelante lo fijaremos en las «dimensiones breves» de estas instituciones (por relación a otras menores o mayores, propia de ciertas composiciones artificiosas)–, pero sin que pudiéramos encontrar alguna razón en esa «dimensión catorce», que en los teoremas va referida a los pasos contados en el plano de los significados conceptuales o proposicionales, y en los sonetos van referidas a los pasos contados en el plano de los significantes, en este caso, en el plano de los significantes prosódicos (ritmo, rima,...) de los versos endecasílabos. Y sin que esta distinción entre ambos planos descarte todo sentido a las cuestiones que, a principios del siglo XX, Eduardo Sievers reunió bajo la denominación de «análisis de los sonidos» (Schallanalyse, descrito en su artículo «Ziele und Wege der Schallanalyse», Heidelberg 1924) como investigación de la influencia de los ritmos de la frase sobre su sentido.
Ahora bien, lo que decimos de las involucraciones sociales y políticas que constatamos en el canon artificioso según el cual se despliegan los teoremas en una época determinada –los teoremas de la Geometría y en general los contenidos del Quadrivium (particularmente los de la música pautada)– podríamos decirlo también de las involucraciones políticas y sociales de los «despliegues canónicos» de los contenidos del Trivium (Gramática, Retórica, Dialéctica) y, en particular, en nuestro caso, de los sonetos, asumidos sobre todo por los gramáticos y por los retóricos, o por una disciplina que reunía a ambos y que solía llamarse Ars dicendi.
En efecto: tampoco la estructura del soneto surgió de golpe. Había cuartetos populares satíricos, serventesios (del provenzal serventes), cuyos versos rimaban alternados según la pauta ABAB. La estructura del soneto clásico de arte mayor (es decir, dejando de lado los sonetos de arte menor, los «sonetillos», con versos de ocho sílabas, o los «sonetos spenserianos» de verso blanco, sin rima), incluido el soneto isabelino inglés (compuesto de tres serventesios y un pareado con la rima ABAB CDCD EF EE GC), se institucionaliza, como hemos dicho, en un ambiente cortesano, concretamente en el de la corte imperial de Federico II Hohenstaufen. Lo que obviamente no quiere decir que fuera el propio emperador el creador del soneto, puesto que tal «creación» fue un resultado de la actividad de cortesanos de origen probablemente plebeyo, como pudo serlo Giacomo da Lentino, notario y diputado legal del emperador, y aún acaso su canciller Pierre de Lavigne (1197-1249). Cortesanos en todo caso conscientes de su puesto en la jerarquía, y de la exigencia que ese puesto imponía en el momento de mantener sus distancias con el vulgo al ofrecer como resultado de sus más preciados «trabajos ociosos» una obra artificiosa y difícil («nobleza obliga»).
Probablemente (como dice Michel R. G. Spiller en The Development of the Sonnet. An introduction, Routledge 1992, pág. 14) sería un anacronismo ver en la corte de Federico algo así como una corte del Renacimiento; pero cuando el emperador se movía a través de las ciudades y de los castillos, requería un control centralizado a cargo de un alto y leal equipo de administradores y profesionales. «De este cuerpo secular habría surgido el invento del soneto». El poder y el control del lenguaje iban juntos, en una sociedad que recibía las tradiciones de la antigüedad grecolatina, de los trovadores provenzales (que florecieron en Francia de 1100 a 1300) o de las «filigranas» árabes de España. El control del lenguaje implicaba la noción y la práctica de la elocuencia, un lenguaje elaborado y distintivo de los hombres refinados frente al lenguaje de un vulgo ineducado, pero muy capaz de envidiar sin embargo la situación privilegiada de los cortesanos de origen no aristocrático. Un vocabulario elevado, de sintaxis compleja, con figuras del lenguaje características. M. Spiller observa que los primeros sonetos en italiano, y por tanto, los primeros en el mundo, surgieron de un ambiente asombrosamente similar a aquel en el que florecieron los primeros sonetos ingleses escritos por Sir Thomas Wyatt (1503-1542) y por el Conde de Surrey (1517-1547) en la corte de Enrique VIII de Inglaterra. Sólo así se explica el proceso de consolidación de un canon tan artificioso como la sucesión, en el soneto, de una octava (rimando en todos los casos ABABABAB) y de un sexteto, variando entre CDE CDE, CDC DCD, &c.
Concluimos, por nuestra parte, observando que si un ambiente aristocrático puede ser condición necesaria para la creación de instituciones tan artificiosas, pero profundas y valiosas, como puedan serlo los mejores sonetos y los teoremas euclideos, sin embargo ese ambiente no es condición suficiente, como lo demostrarían las instituciones protocolarias tan artificiosas como banales y superficiales, por no decir «estúpidas», de la China de los mandarines o del protocolo de saludo en la corte azteca de Moctezuma.
I
Distinción entre instituciones holomórficas e instituciones meromórficas, y estructura noetológica de los «discursos elementales»
1. Atribuimos, en general, racionalidad a las instituciones, a cualquier tipo de instituciones, en general. Y son racionales las instituciones por el mero hecho de ser instituciones, en cuanto este «hecho» implica su sostenimiento, con un mínimo funcionalismo, más allá de la vida de los individuos que las constituyen y las gestionan.
En cualquier caso, las instituciones no son meros «dispositivos» aislados, puesto que están entretejidas e involucradas unas con otras, así como están entretejidos e involucrados con procesos de la «Naturaleza». Sin perjuicio de lo cual, media una cierta confrontación y aún incompatibilidad, más o menos marcada por terceros, entre dos instituciones cualesquiera.
Desde la perspectiva del entretejimiento de las instituciones, y precisamente desde ella, alcanza su pleno significado la distinción que venimos utilizando entre instituciones meromorfas e instituciones holomorfas (vid., por ejemplo, «El puesto del Ego trascendental», El Basilisco, nº 40, pág. 42; y «Teoría de las Instituciones», El Basilisco, nº 37, pág. 32). Porque el hecho de que toda institución esté siempre involucrada con alguna otra no quiere decir que sea una parte de ella (meromorfa o merotética, por tanto).
Hay instituciones que están orientadas, según su finis operis, a constituirse intencionalmente como unidades autónomas, sin perjuicio de su necesaria involucración con otras distintas; pero hay instituciones que según también su finis operis están concebidas intencionalmente como partes (atributivas o sistáticas, pero también distributivas) de otras instituciones.
En general, los todos y las partes de los aquí hablamos son en principio todos sistáticos o atributivos, o partes atributivas, es decir, no son todos distributivos o partes distributivas, que tampoco se excluyen.
Instituciones tales como «tramo» (de una vía ferroviaria), «cruce» (de caminos), «rodilla» (como eslabón entre muslo y pierna), «tejado» (de una casa), «mango» (de una sartén), «volante» (de un automóvil), «tabique» (de un apartamento), o como «apéndice» (de un cuerpo) o «torso» (de una estatua) pueden ser ejemplos de instituciones meromorfas.
Un tramo, como un cruce, por ejemplo, son, en efecto, instituciones cuyo sentido sólo se alcanza en su inserción en una vía o en varios caminos; un tejado o un tabique sólo tienen sentido como partes de una casa, del mismo modo a como un volante sólo se entiende como parte de un automóvil, o un dorso –aunque esté expuesto en solitario en el pedestal aislado de un museo de escultura– es siempre parte de una estatua, como totalidad atributiva (lo que no excluye la posibilidad de «totalizar» distributivamente los torsos conservados en el museo, y asignarles una sala especial; solo que entonces las piezas de esta sala constituirán ante todo una totalidad distributiva, y no atributiva). En términos lingüísticos diríamos: la sala del ejemplo nos ofrecería antes un paradigma escultórico que el eslabón de una cadena.
Pero, en cambio, la «estatua» es ya una unidad holomorfa, sin perjuicio de que, a su vez, forme parte de un edificio, en el finis operantis del decorador; asimismo es holomórfico el automóvil (que sin embargo necesita una pista para rodar); también la casa (aún formando parte del caserío de la ciudad) es una institución holomórfica (la casa es símbolo del Mundo) y podrían, en principio, ser derruidas las restantes casas de su manzana manteniendo su unidad, que viene definida por otro sistema de relaciones distintas de las que mantiene con otras casas. En cambio, un «torso», o un «mango», pierden su significado disociados de la estatua o de la sartén.
En el campo de la literatura, y respecto de las grandes unidades totales (como pueda serlo una epopeya como la Iliada o una novela como La montaña mágica), encontramos pasajes «exentos» o «disociables» que, sin embargo, están integrados a estos grandes textos, de la misma manera a como las estatuas están integradas en el conjunto total de la casa, e incluso pueden transportarse sin detrimento de su integridad a otros edificios. Las cinco vías de Santo Tomás constituyen un «argumentario», es decir, una unidad holomórfica que se diferencia de cada una de las vías utilizada por separado, es decir, como unidades meromorfas.
Desde la perspectiva «trivial» del Ars Dicendi tradicional, el concepto que hemos podido encontrar más afín al de las «unidades holomorfas» ha sido el concepto de periodo. José Kleutgen (1811-1883), que cita como denominaciones diversas [conónimas] de periodo, dentro del vocabulario de Cicerón, a las siguientes: ambitum, circuitum, comprehensionem, circunscriptionem, define el periodo de este modo: «41. Periodus definitur amplior verborum comprehensio, quae per partes inter se apte cohaerentes numerose absolvitur», y supone que a la formación de un periodo concurren tres condiciones: (1) una cierta amplitud de la oración, (2) la copulación de sus partes, y (3) el número, porque el periodo es una «oración numerosa».
Y como parte del periodo –por tanto, como partes de la «cadena»– Kleutgen cita a los miembros (kolon), a los incisos (kommata), a la protasis (antecedente) y a la apódosis (consecuente), que dividen el periodo en dos partes. También distingue Kleutgen dos géneros de periodos: el simple (monocolos) –que puede sin embargo tener incisos–, el bimembre (prótasis, apódosis), el trimembre, el tetramembre (tres prótasis y una apódosis, o una apódosis y tres prótasis). Por otra parte, los periodos pueden amplificarse o comprimirse.
Sin duda, las distinciones de Kleutgen son «de brocha gorda» (acaso porque su perspectiva es proposicional, más que objetual), pero, sin embargo, nos sirven para constatar cómo ha sido advertida la estructura de las instituciones de las que hablamos. No es este el lugar para replantear más a fondo esta cuestión.
En cualquier caso, de entre la enorme variedad existente de instituciones complejas (no «atómicas», monocoloi), aquellas que aquí nos interesa analizar, son las instituciones discursivas (o argumentativas) elementales, es decir, aquellas instituciones que contienen un «discurso exento» o «autónomo» y relativamente breve en el cual quepa constatar de algún modo un «razonamiento», o, como suele decirse, un «pensamiento» (es frecuente que los tratados de Retórica o de la antigua Preceptiva literaria advirtieran, al hablar del soneto, que el soneto consta de catorce versos «en los cuales debe expresarse un pensamiento»; añadiendo que «por ello deben economizar las palabras para que el pensamiento quepa en los catorce versos»), dando por sobreentendido qué sea tal cosa, sin molestarse en aclarar qué pueda significar ese «pensamiento».
Como ejemplo de estas instituciones discursivas elementales pudiéramos poner algunos silogismos aristotélicos o estoicos, pero también las aporías de Zenón, o los dilemas de Protágoras, cuyo nivel de complejidad es superior al de las «instituciones atómicas» (cabría decir que las instituciones discursivas elementales son «moleculares» y no «atómicas»). En cualquier caso, estas instituciones discursivas elementales (moleculares, por ser discursivas), tienen una dimensión intermedia entre la que correspondería a las instituciones «atómicas» –tipo axioma, aforismo, o sentencia– y la que corresponde a instituciones argumentativas masivas (oración forense, discurso político, libro en el que se expone una doctrina completa, como pueda serlo la Fenomenología del espíritu de Hegel).
Es obvio que estas estructuras necesitan un análisis más preciso en el que aquí no podemos entrar.
Sin embargo, como prototipo de instituciones discursivas elementales holomórficas o «moleculares», no dudamos en considerar a los teoremas de Euclides o alguno de los sonetos de Lope de Vega. Y esto sin perjuicio de que grupos de estos teoremas o sonetos puedan constituir subsistemas distributivos en los cuales asumen el papel de partes de una totalidad más amplia.
Los teoremas ofrecen, sin duda, una «argumentación cerrada», que se ha convertido en paradigma del discurso racional, y que, sin perjuicio de su involucración con otros teoremas, es susceptible por tanto de un análisis noetológico.
Precisamente por ello se nos ofrece como un «hecho» interesante el que, no en todos, pero sí en algunos sonetos, podamos descubrir un estrecho paralelismo con los teoremas euclidianos, siendo así que los sonetos son instituciones, racionales sin duda «en su género», pero no necesariamente «argumentativas». Es decir, suponiendo que los sonetos sean instituciones racionales pero de otro género que el de los teoremas, por así decirlo, que no son del género quadrivial, sino del género trivial, como puedan serlo las arias, las coplas, las canciones o la expresión de «pensamientos», desiderativos, descriptivos, irónicos (tipo «érase un hombre a una nariz pegado»).
Se concederá, sin embargo, la posibilidad de que, aunque la mayoría de los sonetos no sean «discursivos», no existe razón alguna para que no pudieran ser argumentativos en algún caso. Y su carácter argumentativo –esta es la idea que queremos subrayar– no nos obligaría a reducirlos a la condición de teoremas geométricos, puesto que la racionalidad no se circunscribe exclusivamente al ámbito de la racionalidad científica, la que (suponemos) nos conduce a verdades apodícticas (entendiendo las verdades como identidades sintéticas). Estamos ante un tipo de racionalidad que podríamos llamar «literaria», o «trivial», pero dotada de una estructura especial.
En nuestro caso: los teoremas de Euclides ofrecen una forma institucional «elemental» (molecular) de expresión de argumentaciones resolutivas en verdades, interpretables como identidades sintéticas. El soneto de Lope de Vega que vamos a analizar (uno de los llamados «mansos») no es, en modo alguno, un teorema, ni nos lleva a ninguna verdad científica, aunque sí acaso a alguna aproximación (práctica-empírica, o de experiencia), a alguna verdad de tipo etológico o filosófico que resulta de una peculiar «experiencia» interpretable por otras personas que no se encuentran en las mismas circunstancias («deja libre a mi manso y verásle cómo viene a mí, si es que aún tienen sal las manos de su dueño»).
No es por tanto lo principal de nuestro intento el constatar el hecho (puesto que lo suponemos posible) de que la forma soneto pueda haber sido utilizada para exponer un discurso argumentativo, incluso en una temática que parece estar a mil leguas de este intento, sino constatar que este hecho permite extender la estructura de lo que llamamos «circuito noetológico elemental» más allá de los teoremas geométricos. Con lo cual quedaría demostrada la distinción entre la «Noetología» y la Teoría de la ciencia o «Gnoseología». Y esto abre múltiples horizontes al análisis de la racionalidad noetológica, y a su confrontación con la racionalidad estrictamente científica, si se quiere, con la racionalidad «poética». En cualquier caso, abre amplios horizontes en el momento de movernos en un terreno en el cual las oposiciones corrientes entre razón/intuición, o razón/sentimiento, se desvanecen.
II
La estructura noetológica de los teoremas euclidianos
1. Ante todo queremos subrayar que la racionalidad de los teoremas euclidianos a la que nos referimos tiene que ver con las figuras que acompañan a su exposición (ya estén incluidas en el texto de cada uno de los teoremas, ya aparezcan en una lámina aparte junto con otras figuras).
Esta observación, que parece obvia, se oscurece por quienes consideran que el trato del geómetra con las figuras es puramente «intuitivo» (sin tomarse la molestia de decir qué entienden por intuitivo), o una mera concesión pedagógica, presuponiendo que la racionalidad no necesita figuras, sino que se mantiene en el terreno de las letras, de símbolos literales (A, B, Γ..., a, b), es decir, del álgebra. Pero las letras de Euclides acompañan siempre a las figuras, determinan sus partes significativas o el todo, y su tratamiento no es en modo alguno intuitivo (inmediato, según lo que Espinosa llamaba «conocimiento de tercer género»), sino precisamente operativo.
Dejando al margen la cuestión general sobre si el razonamiento geométrico necesita o no figuras (como pretenden los matemáticos de inspiración espiritualista, en la línea de Von Staudt), y refiriéndonos a las demostraciones de Euclides, parece innegable la involucración de su discurso con las figuras, y no de modo «intuitivo» (es decir, inmediato) sino discursivo (es decir, mediante operaciones y confrontaciones, incluso silogísticas, de los términos analizados en cada figura).
2. los teoremas euclidianos son unidades relativamente breves cuya exposición, como hemos dicho, suele ocupar en algunas ediciones catorce líneas numeradas. Tantas líneas, casualmente, como las que ocupan los catorce versos endecasílabos del soneto clásico; y se me permitirá confesar que si aludo a esta coincidencia es porque fue precisamente ella la que hace años me dio ocasión para sospechar la afinidad entre sonetos y teoremas.
Pero el encadenamiento acumulativo de las líneas oculta su verdadera estructura, sobre todo cuando se suponía que estas líneas son proposiciones enunciativas y que los teoremas vienen a ser algo así como silogismos aristotélicos encadenados, en función de hipótesis, de tesis, &c. (y esto desde Alejandro de Afrodisia, que supuso que los Elementos de Euclides serían algo así como los Segundos analíticos «puestos en movimiento», hasta el presente, hasta Bochenski o Scholtz, que defendieron esta idea en los años de expansión de la llamada «Lógica de proposiciones»).
El mayor peligro, a nuestro juicio, de las interpretaciones «proposicionalistas» de los teoremas (como si cada teorema pudiera ser reducido a un encadenamiento de aproximadamente catorce proposiciones) es el encubrir la estructura circular, de «circuito», de esta cadena. Es decir, el hecho de que su primer eslabón está ya referido al último (o a los últimos). Circularidad que no es fácilmente explicable a escala proposicional-silogística, inspirada más bien en la imagen del discurso fluvial, un discurso que, como el río, se aleja continuamente de sus fuentes.
Proclo intentó reorganizar las catorce líneas en seis grandes fases que ya hemos citado, pero estas seis fases tampoco ofrecen estructura procesual alguna, y son más bien fases descriptivas «empíricas», obtenidas por el cotejo de diversos teoremas. También Proclo ofreció, como dijimos, una reclasificación más simple en tres fases (enunciación, demostración y conclusión). Pero estas tres fases, dada su vaguedad, no desbordan su horizonte pedagógico: se trata de una fasificación más próxima a la que es propia del análisis retórico de un discurso didáctico o forense. Pero, ¿cómo se encadena la fase primera y la fase segunda, por ejemplo? La enunciación del teorema suele dar nombre al teorema íntegro, y al mismo tiempo suele constituir la primera línea del teorema. Algo así como una primera premisa de la que fueran «manando» las siguientes. Pero la primera línea del teorema (la prótasis) no es una premisa, ni siquiera una proposición enunciativa, con sujeto, cópula y predicado. Por ejemplo, como prótasis del teorema 47 suele considerarse el enunciado siguiente: «En los triángulos rectángulos el cuadrado del lado que subtiende el ángulo recto es igual a los cuadrados de los lados que comprende el ángulo recto». Pero es evidente que este enunciado no puede ser una premisa (un principio, un postulado), puesto que ella no está probada geométricamente (aunque sí empíricamente), sino que es aquello a lo que el teorema llegará en su fase final (sympérasma). ¿Designa este enunciado al teorema íntegro en la totalidad de su curso? Pero entonces no debe figurar como prótasis de la cadena.

Euclides I,47 en la primera edición en español, Sevilla 1576
Sin duda, el enunciado, en cuanto prótasis, se propone como un «objetivo» (teleológico) a establecer –método es camino, pero camino reandado (ver «Homo viator. El viaje y el camino»): en la prótasis de Euclides I,1 se cita la letra Γ antes de haberse dibujado los círculos–, partiendo de la figura obtenida por la acumulación de tres términos (los cuadrados) construidos sobre un triángulo rectángulo no necesariamente isósceles, una figura que suele ser denominada coloquialmente «molino de viento», como figura muy artificiosa (que no se «deduce» en absoluto de cada una de sus partes).
El teorema no trata por tanto de descubrir estas relaciones (que en el caso del teorema I,47 suponemos descubiertas o conocidas en la práctica de agrimensores, albañiles o carpinteros), sino de derivarlas de una figura tan artificiosa como pueda serlo ese «molino de viento» cuyos miembros se sobreañaden de modo contingente al triángulo rectángulo dado. La estructura procesal operatoria del teorema parece consistir de algún modo en una serie de transformaciones encadenadas que, partiendo de una disposición figurativa en la que se constatan empíricamente estas relaciones, acaban reproduciendo –en una transformación idéntica– las mismas relaciones de partida, pero dadas ahora como derivadas necesariamente de la «inmanencia» de la figura artificiosa, convenientemente «troceada», de la que habíamos arrancado.
Y es de esta sucesión de transformaciones encadenadas, que se resuelven en una suerte de transformación idéntica (porque el resultado o sympérasma aparece ya formulado en el inicio, o prótasis), en tanto es generalizable a los teoremas euclidianos, es de donde obtenemos la estructura de un tipo de «circuito noetológico» (como formulación de la más interna y esencial caracterización de los teoremas de Euclides) que consideramos como el prototipo de las transformaciones gnoseológicas o demostraciones científicas en las que se establecen las verdades como identidades sintéticas.
3. Simplificando: las seis fases de Proclo se incorporan dos a dos en las tres etapas del ciclo o circuito noetológico al que nos referimos:
Etapa I. Propuesta o proposición (de composición-segregación), que incorpora las fases (1) Prótasis y (2) Ekthesis.
Etapa II. Contraposición, que incorpora las fases (3) diorismós y (4) kataskeué.
Etapa III. Resolución, que incorpora las fases (5) apódeixis y (6) sympérasma.
4. El término «proposición», con el que denominamos a la etapa I, no tiene por tanto el sentido de «enunciado» (como proposición enunciativa), sino el sentido de una «proposición operativa»; es decir, el de una «propuesta» de composición-segregación de términos o relaciones dadas. El ciclo o circuito noetológico de referencia consta sintácticamente de términos, relaciones y operaciones; la «propuesta» (o proposición) va referida a las operaciones entre términos y relaciones de un campo de referencia.
Suponemos (dada la imposibilidad de términos o relaciones aislados) la implicación estructural entre una composición de términos, por ejemplo, la composición de los tres cuadrados (sobre los lados del triángulo rectángulo dados) y una segregación de estos términos en terceros. Por ejemplo, en el teorema I,47, al determinar los puntos que acotan los segmentos iguales en la recta perpendicular a cada lado del triángulo rectángulo, estamos segregando las semirrectas que se originan a partir de esos puntos «alejándose» de los lados del cuadrado construido.
Y, en la medida en la cual una composición dice siempre segregación significativa, y una segregación dice siempre composición, se comprende la posibilidad de distinguir dos tipos de teoremas que podrían denominarse «teoremas téticos» (por analogía con las operaciones téticas o compositivas, tales como, en Aritmética, la adición, el producto, la potenciación o la integración) y «teoremas líticos» (por analogía con las operaciones líticas o descompositivas, tales como la sustracción, la división, la radicación o la diferenciación). El teorema I,47 citado («levantar tres cuadrados sobre los lados de un triángulo rectángulo») es claramente tético; el teorema I,3 («dadas dos rectas desiguales quitar de la mayor una recta igual a la menor») es lítico.
5. La etapa II, o de contraposición, que incorpora las fases (3) y (4), está impuesta por la involucración material que la figura compuesta-segregada en la etapa I mantiene siempre con otras realidades materiales de su «entorno», que obstaculizan, canalizan, determinan o distorsionan, incluso contradicen a la figura recién establecida o «propuesta». Por ejemplo, si tomamos como diorismós del teorema I,47 la fase (3), que comienza, como en general todo diorismós, por la forma «digo que el cuadrado del lado BΓ es igual a los cuadrados de los lados que comprenden el ángulo recto», vemos que estamos segregando el cuadrado de lado BΓ (la hipotenusa) de los cuadrados levantados sobre los lados BA y AΓ, pero una vez que el triángulo rectángulo BAΓ hubiera girado en torno a BΓ, como en torno a un eje, hasta situarse, por ejemplo, en un plano perpendicular al que contiene el cuadrado BΓΔE. Asimismo el diorismós segrega el triángulo rectángulo BAΓ de partida de la circunferencia de centro O (que divide a BΓ en dos segmentos iguales) y radio BO = OΓ, circunferencia que contiene al triángulo de referencia como triángulo diametral, y que pasa por los tres puntos B, A, Γ; y lo contiene no accidentalmente, sino como contexto necesario en virtud del recíproco del primer teorema atribuido por Proclo a Tales de Mileto («todo triángulo inscrito en una circunferencia que tenga como diámetro uno de sus lados, es rectángulo». Remitimos a nuestra La Metafísica presocrática, págs. 64-65).
Por lo demás tales segregaciones (que en general implican que toda composición es al mismo tiempo una destrucción) son muy pertinentes cuando las consideramos desde la perspectiva de las determinaciones del «contexto determinante», por ejemplo, el implícito en el teorema I,47, a saber, el plano uniforme en el que se componen los tres cuadrados que integran el «molino de viento» y las relaciones directas (por ejemplo las rectas que corresponden al contexto determinante en la fase 4, de kataskeué).
Según esto el diorismós 3 establece aquí el contexto determinado que define la «condición de posibilidad» del teorema; y la kataskeué 4 establece el contexto determinante de las relaciones que brotarán de la «inmanencia» de las figuras simbolizadas en el artificioso «molino de viento» (que es cualquier cosa menos un unum per se o una «naturaleza eterna» de las exigidas en la teoría de la ciencia antigua y escolásticas para las demostraciones científicas).
Por tanto, la kataskeué no es una mera reexposición del diorismós, sino que es, ante todo, una primera reconstrucción, con regla y compás, sobre las líneas dadas en la ekthesis, apoyada en problemas y teoremas anteriores, concretamente: el teorema 46 («a partir de una recta trazar un cuadrado»), el 34 («los paralelogramos tienen lados y ángulos opuestos iguales») y el 29 («la recta que incide sobre dos paralelas hace los ángulos alternos iguales»). Tras esta primera construcción (que introduce los esquemas materiales de identidad, tales como rectas, rectángulos, paralelas, ángulos rectos, cuadrados, &c.) viene una descomposición o despiece del cuadrado mayor en rectángulos parciales: «trácese AΛ paralela a las dos rectas paralelas BΔ y ΓE». Una descomposición que mantendrá la sinexión de las rectas. Finalmente la kataskeué se termina, en el teorema 47, con la recomposición de dos rectas (AΓ y AH) en una misma recta: «El ángulo BAΓ es recto» –es decir, en cuanto tal– y es recto el BAH (por construcción); por lo que en virtud del teorema I, 14, AΓ y AH (cuyos adyacentes son dos rectos) formarán parte de la misma recta.
6. El ciclo (o circuito) acaba en la tercera etapa (resolutiva), que incorpora las fases (5) apódeixis y (6) sympérasma. En esta etapa se establecen las relaciones entre las partes que determinan las figuras intermedias; es aquí cuando puede entrar en acción los «silogismos autológicos de sustitución» (apódeixis) –es decir, silogismos entre términos que no son elementos de clases distributivas sino partes de totalidades atributivas (como atributivos son, aunque no sean reconocidos por tales por quienes los interpretan como meros recursos didácticos dirigidos «a una princesa de Alemania», los términos de los silogismos representados por los círculos de Euler)– y, en el sympérasma alcanzan, tras la segregación de las figuras auxiliares que desempeñan el papel de términos medios de silogismos atributivos, la identidad sintética, la verdad, entre las suma de las áreas de los cuadrados de los catetos y el cuadrado de la hipotenusa. El sympérasma tiene sin duda mucho de conclusión, pero no en el sentido de un resultado «desprendido» (el término medio no debe entrar en la conclusión) de una larga cadena de premisas, sino en el sentido de una «recuperación» de la propuesta inicial de la prótasis, que precisamente se reproduce en la conclusión, y no como un mero «caso particular suyo».
7. El ciclo noetológico en tres etapas podría ponerse en correspondencia con el silogismo de Aristóteles (dos premisas y una conclusión) y con las triadas de Hegel (tesis, antítesis, síntesis). Sin embargo el ciclo noetológico no se reduce al silogismo aristotélico, como hemos dicho, porque éste se mantiene en el terreno de las clases distributivas y el circuito noetológico se mantiene entre clases en principio atributivas. Tampoco cabe reducir el circuito noetológico a las triadas hegelianas, porque en éstas la tesis asume la forma de una proposición enunciativa, y la antítesis se presenta como negación global o externa, siendo así que la contraposición no es una mera negación proposicional externa y global de la propuesta (tipo «el hombre es mortal»/«el hombre es inmortal»), sino un desarrollo interno del contexto involucrado. Cabría, en cambio, reducir los silogismos y las triadas a la condición de expresiones simplificadas (y aún degeneradas) de circuitos noetológicos.
8. El análisis noetológico de los teoremas de Euclides permite también dar cuenta, con toda facilidad, de la distinción tradicional entre los teoremas y los problemas, así como delimitar el alcance de esta distinción.
La distinción entre teoremas y problemas tiene como «fundamento filológico», emic, las formas utilizadas en la resolución o sympérasma de cada «proposición». Como ya hemos dicho, los problemas se reconocen por la fórmula ὅπερ ἔδει ποιῆσαι («como había que hacer») y los teoremas por la fórmula ὅπερ ἔδει δεῖξαι («como había que demostrar»).
Ahora bien, es obvio que este criterio es muy poco significativo desde un punto de vista gnoseológico, porque presupone una oscura distinción entre el hacer (ποιῆσαι) y el demostrar (δεῖξαι), cuyo significado gnoseológico permanece indescifrado. Si el hacer tiene que ver gnoseológicamente con operaciones (¿acaso no hay tantas operaciones en los teoremas como en los problemas?) sólo acudiendo a criterios metafísicos (del estilo: «el hacer va referido al mundo sensible, práctico y corruptible; el demostrar va referido al mundo inteligible, al mundo del conocimiento especulativo de las esencias incorruptibles») cabría dar algún sentido a la distinción entre el hacer práctico y el hacer especulativo (¿acaso el «molino de viento» no es tan «corruptible» como el triángulo rectángulo simple?).
Una distinción que arrastra o contamina a otras distinciones, y que presupone, por ejemplo, la distinción ente las clase de los artesanos (es decir, de las artes mecánicas o serviles) y la clase de los hombres libres (dedicados a las artes liberales). Desde la perspectiva de esta distinción, los problemas tendrían que ver con los asuntos de los artesanos (carpinteros, albañiles), mientras que los teoremas serían asunto de aristócratas ociosos (que se dedican a hacer dibujos sin herirse o mancharse las manos con clavos o con barro). Pero cuando retiramos este contexto parásito (aunque muy activo en múltiples coyunturas sociales históricas) ya no cabe seguir sosteniendo que los geómetras puros que dibujan teoremas con regla y compás fueran más contemplativos que los carpinteros que construían muebles con tablas y clavos; porque los geómetras, con su regla y compás «trabajaban» tanto como los carpinteros con sus tablas y sus clavos. Simplemente se trataba de dos «oficios» diferentes, muy emparentados, por no decir que idénticos, en su principio, pero del cual saldrían diferencias «gremiales» muy distintas. Y si al principio los carpinteros parecían dedicados a tareas más prácticas, mientras que los geómetras –o la casta sacerdotal a la que se refiere Aristóteles– parecían estar rellenando su ocio con juegos inútiles, al cabo de los tiempos resultará que en las sociedades más desarrolladas (desde el punto de vista arquitectónico, industrial o militar, cuando se han descubiertos las máquinas de lanzamiento de proyectiles), el «gremio de los geómetras» alcanzaría una importancia práctica incomparablemente mayor que la que pudiera atribuirse al gremio de los carpinteros. No es de extrañar que los Elementos de Euclides fueran utilizados sobre todo por arquitectos y militares: tenemos a la vista, por ejemplo, la edición de los Elementos geométricos del famoso philosopho Euclides megarense, preparada por don Sebastián Fernández de Medrano (1646-1705), «sargento general de batalla y director de la Academia Real y Militar de los Países Bajos», autor también de El architecto perfecto en el arte militar (Bruselas 1700).
Por lo demás, las interpretaciones de la distinción entre teoremas y problemas en Euclides han adolecido de ausencia de criterios propiamente gnoseológicos, tanto cuando tendían a atenuar y aún a borrar la distinción, como cuando tendían a acentuarla.
En efecto, unas veces se tendió a borrar la distinción, defendiendo la equivalencia estructural de problemas y teoremas, bien fuera desde el supuesto (que seguía la inspiración platónica de Espeusipo), de que los problemas eran en realidad teoremas (acaso versiones pedagógicas suyas) o bien desde el supuesto (que seguía la línea más aristotélica de Menechmos) de que todas las proposiciones de Euclides debieran llamarse problemas, ya construyan la cosa buscada, ya la consideren como un objeto preexistente (por ejemplo, un triángulo rectángulo).
Posidonio, en cambio, defendió la distinción y trató de explicarla desde criterios metafísicos o en todo caso extragnoseológicos: los teoremas tendrían que ver con las esencias (y de ahí su carácter apodíctico), mientras que los problemas tendrían que ver con las existencias. Y por ello, al teorema se opone lo absurdo, pero al problema sólo lo probable.
Proclo, aún utilizando criterios metafísicos, sugería que los problemas de Euclides tienen un contenido que es tan eterno como los teoremas, y que sólo cuando nos situamos no ya en la perspectiva objetiva de los teoremas mismos, sino en la perspectiva del conocimiento que los sujetos pueden tener de ellos, cabría decir que los problemas implican generaciones, divisiones, sustracciones o adiciones de figuras, y por tanto cambios que en ellos se producen.
Sin duda, la distinción entre problemas y teoremas se cruza con otras muchas distinciones y cuestiones, como puedan serlo la distinción entre el ordo inventionis (o los «contextos de descubrimiento») y el ordo doctrinae (o los «contextos de justificación»). Contextos en los cuales tiene lugar (en las ciencias alfa operatorias) la segregación de las operaciones, que pone entre paréntesis el tiempo, siendo así que la geometría segrega el tiempo aunque conserve el movimiento (los desplazamientos, giros, rotaciones o proyecciones de las figuras).
Acaso las cuestiones filosóficas más importantes que latían en el fondo de la distinción entre teoremas y problemas tuvieran que ver con la cuestión de los fundamentos de la necesidad asociada a la verdad de las proposiciones geométricas. ¿Acaso las «verdades necesarias» de la Geometría no requerían el reconocimiento de una «Naturaleza eterna», de un cosmos organizado según las leyes eternas que le imprimió su Demiurgo, entendido a su vez, desde los pitagóricos hasta Kepler o Minkowski, como un matemático?
A su vez, este esencialismo metafísico, ¿acaso no podría interpretarse como una respuesta a la paradoja de que las verdades necesarias ofrecidas por la Geometría euclidiana pudieran derivarse de composiciones-segregaciones de figuras tan artificiosas y contingentes como pudiera serlo la figura base de las demostraciones del teorema de Pitágoras por Euclides, que venimos designando como «molino de viento»?
Es decir: si las verdades científicas se presentan como necesarias, ¿no requieren un fundamento trascendente al Universo cambiante en el que nos movemos? Y si las consideramos referidas a este universo, ¿no deben dejar de reconocerse como necesarias? ¿Habría que recurrir a las no menos metafísicas formas a priori (a priori respecto de las operaciones) de los sujetos humanos? ¿No sería suficiente fundar las relaciones intemporales de identidad que nos arroja el teorema de Pitágoras, no ya desde luego en una figura tan artificiosa como pudiera serlo el «molino de viento», sino en las circunstancias de que este artificio comienza por levantar operatoriamente figuras que contienen esquemas de identidad, por ejemplo, cuadrados con lados iguales, sobre los lados de un triángulo rectángulo? Si las relaciones obtenidas sobre términos gráficos singulares M1 (entre los cuales debe ser posible hacer ajustes o efarmoxis, según la noción común 7: «Y las cosas que coinciden –εφ-αρμόζοντα– entre sí son iguales entre sí») entre las unidades figurativas aliteradas por letras mayúsculas o minúsculas tales como A, B, Γ, H... (que Reviel Netz ha estudiado minuciosament en su libro The Shaping of deduction in Greek Mathematics, Cambridge University Press 1999), pueden asumir un carácter universal, es debido a la capacidad para reproducirse indefinidamente por obra del sujeto operatorio M2 en cualquier dominio del espacio-2 infinito (es decir, en M3).
En cualquier caso, del fundamento que hemos dado a la etapa primera del circuito noetológico, a saber, la propuesta de composiciones-segregaciones entre términos y relaciones, cabe obtener un criterio muy claro para establecer la distinción entre problemas y teoremas. En efecto: cuando partimos de una dada disposición de relaciones, y nos proponemos determinar una composición determinada (una figura) a partir de la cual estas relaciones pudieran derivarse necesariamente, nos encontraríamos con los problemas; cuando partiéramos de una composición segregación de términos dados (de una figura) y nos propusiéramos derivar de ellas necesariamente ciertas relaciones, nos encontraríamos con los teoremas. Y, habida cuenta del dualismo (como cabría llamarlo) que media entre las relaciones y los términos, tendríamos que reconocer el alcance limitado que conviene a esta distinción entre teoremas y problemas, distinción que puede llegar a borrarse en algunas fases del curso del ciclo, y principalmente en la fase kataskeué de su tercera etapa.
III
Sobre la estructura noetológica
del soneto CLXXXVIII de Lope de Vega
1. Asumimos este soneto, en principio, en su sentido literal, no alegórico. Nuestro propósito es aclarar la naturaleza de la afinidad que percibimos oscuramente entre la «argumentación» del teorema I,1 –teorema que en realidad es un problema: «construir sobre un segmento de recta AB un triángulo equilátero»– y la «argumentación» que se contiene, sin duda, en el soneto de Lope de Vega, «Suelta mi manso...». Afinidad que, sin perjuicio de la heterogeneidad de los campos o escenarios respectivos –un campo o escenario geométrico (en el que figuran puntos, segmentos, círculos... de un plano) y un escenario antropológico (en el que figuran toros mansos, mayorales, esquilas de estaño o collares de oro) parece fundada en la analogía entre sendos procesos de transformaciones idénticas que tienen lugar, en todo caso, en campos o escenarios de estructura muy compleja en la que están implicados varios «principios», de suerte que las transformaciones idénticas de los contenidos considerados en estos campos o escenarios no son obvias y exentas, sino que sólo pueden reconocerse advirtiendo caminos análogos entre estructuras tan heterogéneas.

Euclides I,1 en la primera edición en español, Sevilla 1576
En cualquier caso, la razón de haber escogido el teorema I,1 entre otros posibles, en el momento de llevar a cabo la confrontación entre el soneto de Lope y los teoremas de Euclides, es obviamente de orden sintáctico, y tiene que ver con la semejanza en «nivel de complejidad» entre los términos y relaciones que constituyen las estructuras semánticas respectivas. En efecto, el teorema se establece entre dos puntos A y B, extremos de un segmento de recta, «finito y corto» (puesto que ha de ser representable en una figura incluida en un texto); puntos que inmediatamente asumen el papel de centros de dos circunferencias, en cada una de las cuales podemos determinar puntos virtuales en número indefinido, entre los cuales seleccionamos los puntos Γ y Γ’, que pertenecen a la vez a ambas circunferencias. Las relaciones (de igualdad), en torno a las cuales se organiza el teorema, se establecen primero entre los centros A y B, y después entre el punto A y Γ (o Γ’) y entre el punto B (con Γ o Γ’).

El soneto CLXXXVIII de Lope en la edición de Madrid 1776
Pero el soneto que analizamos también se establece sobre dos términos, A y L (Alcino y el locutor o el autor), alrededor de los cuales «giran» los mansos (virtualmente en número indefinido, que pacen en una dehesa también indefinida), entre los cuales seleccionamos los dos que pertenecen a la vez (por querencia o por cautividad) a los mayorales o pastores (Γ y Γ’), o que mantienen relaciones de igualdad recíproca (el manso situado en A, respecto de B, y el situado en B respecto de A).
Supuesta esta estructura sintáctica (de términos y relaciones) similar, se facilita la confrontación de las operaciones de «transformación idéntica» de unas relaciones dadas entre puntos con otras.
Transformaciones idénticas que en todo caso son ante todo transformaciones, que implican cambios, movimientos; por tanto, que no se reducen a la mera relación de reflexividad desde la que suele representarse la idea de identidad (A=A, o Yo=Yo, de Fichte). Cuando hablamos de la transformación idéntica del cuadrado Q «en sí mismo» no nos estamos refiriendo a la supuesta relación «estática» Q=Q, sino a la rotación de 360º mediante la cual Q, desde una posición inicial dada, recupera, tras perderla, la situación originaria mediante el ajuste perfecto o efarmoxis que Euclides prescribía en su séptima noción común del libro I: καί τά έφαρμόζοντα έπ’άλλήλα ίσα άλλήλοις έστιν (las cosas que ajustan [que coinciden, que son congruentes] entre sí son iguales entre sí).
Expondremos la afinidad o analogía, advertida oscuramente, entre el problema y el soneto de referencia desde dos «escalas» diferentes: la primera podría denominarse «conspectiva» o global (otros preferirían definirla como intuitiva, dinámica o sintética); mientras que la segunda se mantiene en una perspectiva más bien analítica, detallada, orientada, en nuestro caso, a delimitar las tres etapas y las seis fases que hemos tenido en cuenta en las secciones precedentes de este rasguño.
La «exposición conspectiva» acaso ofrece lo más esencial del proceso de transformación idéntica, pero al no detallar los pasos del proceso, nos deja muy lejos de los textos que confrontamos (el texto del teorema y el texto del soneto). En cambio, la exposición analítica detallada induce el peligro de perder la visión de la transformación de conjunto. Según esto podría concluirse que ambas escalas son complementarias, y que cada una de ellas «pide» o agradece la otra.
2. Ante todo, la interpretación «conspectiva» de la argumentación del problema I, 1 de Euclides como dispositivo para el desarrollo del proceso de transformación idéntica de un segmento dado en otros dos segmentos convergentes que forman triángulo equilátero con él (o bien la transformación idéntica del segmento AB «existente» en el mismo segmento en cuando lado de un triángulo equilátero).
Partiendo de un segmento AB de recta, dado en el espacio-2, uniforme, isótropo e indefinido (el plano), en el que suponemos dados o determinables infinitos segmentos «virtuales», iguales en longitud al segmento AB, en los cuales podría transformarse éste idénticamente (según el criterio de la efarmoxis) en sus movimientos de rotación del segmento AB (bien sea tomando como centro al punto A o al punto B), nos proponemos «seleccionar» dos de estos infinitos segmentos, que constituyen el conjunto de radios contenidos en los círculos de centro A o B, tales que, mantenido el contacto puntual con un extremo de AB, mantengan también un contacto puntual con el punto Γ común a ambos, formando así un triángulo equilátero AΓB sobre AB, susceptible (el triángulo) de ser visto como un «desdoblamiento» triple del segmento AB obtenido en el curso de su rotación.
(La propuesta de transformación idéntica de AB en los otros dos segmentos que forman el triángulo equilátero puede resolverse de modos distintos y no excluyentes: o bien tomando el punto Γ de intersección de las circunferencias de centros AB y radio AB, o bien tomando el punto Γ’ de la intersección opuesta.)
3. Expondremos ahora la «interpretación conspectiva» de la argumentación en la que haríamos consistir el «pensamiento» contenido en el soneto de Lope de Vega, entendido como un dispositivo para el desarrollo de un proceso de transformación idéntica del manso mA (manso de Alcino) en el manso mL (manso de Lope o de su locutor literario).
Suponemos, refiriéndonos en principio a la estructura del escenario, que la identidad de los mansos m, m’, m’’... no es absoluta, porque un animal sólo adquiere la condición de manso cuando se considera vinculado a su dueño o «girando» en torno a su dueño, así como recíprocamente. Por ello la separación constituye una suerte de mutilación del dueño o del manso (Covarrubias, en su Tesoro, que recoge el lenguaje español de la época de Lope, define así: «De los animales aquellos se llaman mansos que se dejan tratar y palpar con la mano»; y añade: «Díjose manso a manu, porque viene a comer a la mano del pastor»).
Supondremos en segundo lugar (y también en referencia a la estructura del escenario) que la «composición» o vinculación del manso a su dueño (mX) puede ser superficial o externa (cuando hay coacción o engaño, es decir, cuando m no es libre) o puede ser profunda o interna (es decir, cuando deriva de la misma «esencia» o «querencia interna» del manso).
Supuestas estas cosas (entre otras) cabría exponer conspectivamente el argumento del soneto de Lope de Vega de este modo (teniendo en cuenta que los supuestos están implícitos en el soneto; por ejemplo en su primer verso, «Suelta mi manso», el autor o locutor del soneto comienza refiriéndose a un manso como suyo, es decir, vinculado internamente a él):
Partiendo de una situación de composición superficial del manso al mayoral A (Alcino), se plantea la propuesta de la «transformación idéntica» –es decir, de una transformación que mantenga la identidad sustancial de m– de mA en mL, mediante la liberación, suelta o libertad-de de m respecto del mayoral A (que lo mantiene cautivo, «alienado», mediante «engaños»). Una liberación que hará posible la recuperación, por parte de M, de su esencia o libertad-para, que le conducirá espontáneamente (por querencia) a «componerse» con L (con el autor, Lope, o si se quiere, con el locutor textual del soneto). Ahora bien, como la separación de m respecto de mA, al componerse con L en mL determina una «mutilación» de A, que puede ser obstáculo para la transformación, se «compensa» con una transformación recíproca (m’L)→(m’A).
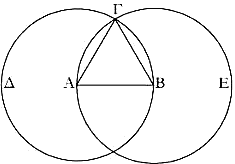
4. La exposición detallada de la afinidad noetológica entre el teorema I,1 de Euclides y el manso de Lope de Vega la ofrecemos a doble columna, a fin de facilitar el cotejo, y previamente damos en español los textos literales.
| Texto literal (no alegórico) cuanto al significado del teorema de Euclides I,1 | Texto literal (no alegórico) cuanto al significado del soneto de Lope (manso canónico) nº CLXXXVIII |
|
 |
||
| Sobre una recta delimitada construir un triángulo equilátero (τρίγωνον ίσόπλευρον). Sea la recta delimitada AB. Se trata de construir sobre la recta AB un triángulo equilátero. Con centro A y radio AB descríbase un círculo BΓΔ. Y de nuevo, con centro en B y con radio BA descríbase el círculo AΓE. Y desde el punto Γ en el que se cortan mutuamente ambos círculos trázense hasta los puntos A y B las rectas ΓA y ΓB. Y puesto que el punto A es centro del círculo ΔΓB, la recta AΓ es igual a la AB. Y asimismo, puesto que el punto B es centro del círculo ΓAE, la recta BΓ es igual a la BA. Pero ya se había probado que la ΓA es igual a la AB. Por tanto cada una de las rectas ΓA u ΓB es igual a la AB. Cosas iguales a una tercera son iguales entre sí. Luego la recta ΓA será igual a la ΓB. Por tanto las tres rectas ΓA, AB y BΓ son iguales entre sí. Luego el triángulo ABΓ es equilátero, y está además construido sobre AB. Q. E. F. |
Suelta mi manso, mayoral extraño, pues otro tienes de tu igual decoro, deja la prenda, que en el alma adoro, perdida por tu bien y por mi daño. Ponle su esquila de labrado estaño, y no le engañen tus collados de oro, toma en albricias este blanco toro, que a las primeras hierbas cumple un año. Si pides señas, tiene el vellocino pardo encrespado, y los ojuelos tiene como durmiendo en regalado sueño. Si piensas que no soy su dueño, Alcino, suelta, y verásle, si a mi choza viene, que aun tienen sal las manos de su dueño. |
Teniendo a la vista esta doble columna constatamos cómo en la primera sección del discurso (propuesta o pro-posición en Euclides, primer cuarteto en Lope), el autor-locutor comienza pidiendo como postulado imperativo (mejor que hipótesis o que axioma) la realización de una operación en el sentido estricto de transformación de entidades corpóreas dadas en contextos determinantes, mediante dos apelativas operacionales: «¡Construye un triángulo equilátero!» «¡Suelta mi manso!».
En la segunda sección (contraposición en Euclides, segundo cuarteto en Lope) se indican las composiciones y separaciones que es preciso establecer en el ámbito del contexto determinado («Traza con centro A y radio AB el círculo BΓΔ», «Ponle su esquila de labrado estaño...»).
La tercera sección (resolución-apódeixis en Euclides, primer terceto de Lope) contiene la demostración, el argumento que ofrece las razones, dentro del contexto determinado, que hace que, puesta la hipótesis inicial, se cumpla, no por una arbitraria decisión, sino por la naturaleza de las cosas («Los segmentos ΓA y ΓB son iguales y ambos lo son a AB», «El manso, cuando está cautivo y cuando quea libre, se mantiene idéntico a sí mismo, en equilibrio, pues aunque esté soñando, su querencia efectiva es otra»).
Y la resolución-conclusión (sympérasma en Euclides, segundo terceto en Lope) ofrece el eslabón que cierra el círculo discursivo, y que, por tanto, no es mera re-petición autológica de la propuesta inicial, sino la re-producción de esta propuesta a partir del seno mismo del teorema. La clave está, por tanto, en el «por consiguiente» o «según esto», ergo, igitur (Επί τής δοθείσης άρα...) que antecede a la reproducción de la conclusión.
Por ello la asombrosa estilística del verso 13 –«suelta y verásle si a mi choza viene»– en lugar de un posible «suéltalo y verás...» (que el metro además prohibía), refuerza la idea de que es el manso mismo quien acude a las manos de su dueño, y no meramente que verá quien lo ha soltado cómo él acude allí, como podía haber acudido a otro lado: «suelta y verásle [a él mismo]». Precisamente porque verás cómo es él quien viene a mi choza (le verás a él, él es el que viene, no sólo tú le ves venir), tendrás que admitir que yo soy su dueño, que es mi manso, como dije el primer verso, Q. E. F.
La confrontación global que acabamos de bosquejar entre la «proposición poética» (problemática) de Euclides y el poema demostrativo de Lope será suficiente, para los fines de este ensayo: analizar cómo las funciones de conocimiento ejercidas en un circuito discursivo de Euclides puede ser atribuidas también de algún modo a uno de los más asombrosos poemas escritos en lengua española. Con esto estamos afirmando que la estructura discursiva del manso canónico de Lope ha de implicar algún tipo de conocimiento verdadero, por precario que sea (comparado con el conocimiento apodíctico del teorema geométrico).
Un tipo de conocimiento que nos presenta (en la interpretación alegórica que vendrá tras la interpretación literal) a los seres humanos en cuanto sometidos por encima de su voluntad y de su libertad a leyes ineluctables que manan de su propia naturaleza.
Si quisiéramos detallar aún más la confrontación (sin «castigar» excesivamente el sentido de los textos), obtendríamos acaso un cuadro como el siguiente (en el que las correspondencias, si se aceptan de algún modo, no dejarán de producir asombro a los partidarios de la dicotomía absoluta entre las ciencias y las letras (o, si se prefiere, a la dicotomía pascaliana entre el esprit de géométrie y el esprit de finesse.
| Etapas | Fases | Teorema I,1 de Euclides | Soneto CLXXXVIII de Lope | |
| I Propuesta (composición/ segregación) |
(1) Prótasis Propositiva |
Construye un triángulo equilátero sobre una recta delimitada | 1 Suelta mi manso, mayoral extraño, 2 pues otro tienes de tu igual decoro, |
|
| (2) Ekthesis |
Es decir, sobre la recta AB construye un triángulo equilátero |
3 deja la prenda, que en el alma adoro, 4 perdida por tu bien y por mi daño. |
||
| II Contraposición |
(3) Diorismós |
Describe un círculo AΓΔ con centro en A y radio AB...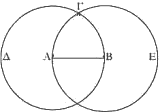 |
5 Ponle su esquila de labrado estaño 6 y no le engañen tus collados de oro, |
|
| (4) Kataskeué |
A partir del punto Γ donde los círculos se cortan traza dos rectas formando el triángulo AΓB y el círculo BΓE, &c.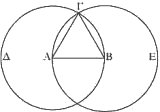 |
7 toma en albricias este blanco toro, 8 que a las primeras hierbas cumple un año. |
||
| III Resolución |
(5) Apódeixis |
A es el centro del círculo ΓΔB; luego AΓ es igual a AB [por la definición 5], B es el centro del círculo ΓAE, luego BΓ es igual a BA [definición 15]; luego ΓA y ΓB son iguales a AB; luego [noción común 1: dos cosas iguales a una tercera son iguales entre sí] los tres segmentos de rectas son iguales entre sí. | 9 Si pides señas, tiene el vellocino 10 pardo encrespado, y los ojuelos tiene 11 como durmiendo en regalado sueño. |
|
| (6) Sympérasma |
Luego el triángulo ABΓ es equilátero y construido sobre la recta delimitada AB. Q. E. F. 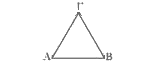 |
12 Si piensas que no soy su dueño, Alcino, 13 suelta, y verásle, si a mi choza viene, 14 que aun tienen sal las manos de su dueño. |
5. Comentarios al precedente análisis del teorema y del soneto.
| a) El teorema (problema) es tético, no analítico. Propone (en forma traducible por un imperativo o por un apelativo) levantar o edificar un triángulo equilátero a partir de alguna recta delimitada por dos puntos. La propuesta puede interpretarse como un imperativo impersonal («hágase»), pero el destinatario de la propuesta es desde luego un sujeto operatorio humano, y un sujeto operatorio que debe ponerse a dibujar, a actuar. Dicho de otro modo: la prótasis del teorema se dirige al lector, con la intención de implicarle («de hacerle cómplice», si el requerimiento fuese delictivo) en el asunto. Aquí cabe poner una diferencia esencial entre una propuesta geométrica y una propuesta contenida en un texto literario. Diferencia paradójica si se da por supuesto que los propios geómetras prescinden del tiempo, son «intemporales» («eternos»), y que, por tanto, no tienen por qué tener en cuenta a los mortales que les contemplan. ¿No obligaría esta sola dificultad a retirar la interpretación contemplativa del oficio matemático? O, al menos, a distinguir, en el eje sintáctico, entre los componentes operatorios de la Geometría (que son subjetuales, por implicar al sujeto operatorio) y sus componentes objetuales (términos y relaciones). En todo caso una cosa es el proceso de neutralización o segregación del sujeto operatorio (en las disciplinas α-operatorias) y otra cosa es la sustantivación o hipóstasis de los campos científicos (y en particular de los campos geométricos). |
a) El soneto comienza con un «imperativo lítico» («Suelta», con el sentido de «libera de»). Quien formula apelativamente esta propuesta imperativa es el sujeto literario inmanente al texto que llamamos «el locutor», y que sólo por caminos extratextuales o extraliterarios, le ponemos el nombre de Lope de Vega. En cualquier caso, la principal diferencia con la prótasis del teorema habrá que ponerla en este punto: el destinatario de la prótasis imperativa del teorema es un sujeto operatorio extratextual (el lector), mientras que el destinatario de la prótasis imperativa formulada por el locutor, es otro contenido literario, el «mayoral extraño». A él se dirige la intimación, no al lector, que habrá de limitarse a contemplar «en tercera persona» cómo alguien, el autor-locutor, da la orden a alguien de que ponga en libertad a un toro manso, al mismo tiempo que le insinúa desde el principio que lo tiene cautivo («mayoral extraño») y le recuerda («por simetría») que él ya tiene otro toro manso de igual decoro. De este modo se establece la simetría entre el locutor y el destinatario, por lo que habría que suponer que el destinatario debe darse por satisfecho. Aquí podría verse el indicio de una «línea de fractura» de la consistencia del soneto. Porque si al mayoral extraño se le considera satisfecho en el verso 2 no habrá por qué ofrecerle el regalo en el verso 7; en todo caso, el verso 7 desvirtúa la conminación de arranque del verso 1. El mayoral extraño debe soltar a su manso «por la naturaleza de las cosas», pues la libertad que el locutor pide para el manso cautivo es una libertad-para, para que el manso liberado vaya a su dueño, que es el que ordena la liberación (de modo parecido a como el radio AΓ y el radio BΓ concurren por sí mismos en un punto Γ). Se salvará la inconsistencia interpretando (sin duda de un modo algo forzado) el «tienes» del verso 2 como un «tienes a tu disposición» el toro blanco de 7. Y, sobre todo, quedaría justificada la información que se da en 8: «advierte que el toro que te daría en albricias es un manso joven, cuya querencia hacia tí nacerá de una situación virgen y genuina (como la querencia que mi manso tiene hacia mí, aunque tú lo mantengas cautivo)». |
|
| b) La característica de la implicación que acabamos de señalar arroja luz sobre el significado de la ekthesis del teorema I, 1. Desde otro punto de vista podría pensarse que el presentar en (2) la recta delimitada AB es una mera reiteración de la prótasis (1), justificada a lo sumo como un redundante recurso pedagógico. Pero esto no es así: la ekthesis no es una mera redundancia de la prótasis, ni menos aún (como algunos sugieren, entre ellos García Bacca) la prótasis es una hipótesis (o el antecedente) y la ekthesis como tesis (o el consiguiente). Como si estuviéramos ante una concatenación de proposiciones propia de las ciencias hipotético-deductivas. Pero la ekthesis no es una «deducción» de la prótasis. Es una «reconfiguración morfológica» de un material previo lisológicamente presentado, y, a la vez, es la transformación de una totalidad distributiva (la «recta delimitada», una cualquiera entre las infinitas) en una totalidad atributiva (el segmento AB). En efecto, la recta delimitada de la prótasis es infinita, por lo que la delimitación de extremos en ella no rebasa el alcance de un concepto distributivo. La ekthesis delimita, en cambio, el segmento marcando los extremos precisos A, B. Es decir, establece mediante letras una unidad operatoria (las letras A, B señalan una unidad bidimensional finita mediante la separación de otras, señalando sus puntos extremos). La propuesta de un triángulo equilátero, que la prótasis mantiene sin parámetros, es un campo no operatorio –la delimitación de las rectas podría tener lugar tanto si la distancia entre A y B tendiera a cero como si tendiera a infinito, es decir, a valores no operatorios– que se transforma por la ekthesis en una proposición operatoria. |
b) Tampoco los versos 3 y 4 constituyen una mera reiteración (acaso añadiendo algún matiz enfático) de los versos 1 y 2. En estos versos el autor-locutor añade algo esencial: que mi manso no es mío en un sentido meramente jurídico o económico (acaso, por ejemplo, porque fue fruto de la ganadería de la dehesa) –es decir, desde un punto de vista lógico, en el sentido distributivo de «cualquier fruto de mi hacienda»– sino que es mío como parte singular (idiográfica) de mi alma, y por ello le adoro. Y aún más: el verso 4 añade que este manso, eligiendo idiográficamente y segregándose del conjunto indefinido de los mansos virtuales que lo envuelven (como la ekthesis del teorema I, 1 identificaba y segregaba el segmento AB del conjunto de los infinitos segmentos) no solamente es diferente de los demás, sino que él ha sido la causa del enfrentamiento del mayoral extraño y del efectivo dueño. | |
| c) El diorismós del teorema amplía el contexto determinante de los segmentos precedentes. El segmento AB está dado dentro de un espacio o conjunto infinito de segmentos iguales (entre los cuales habrá que seleccionar los dos necesarios para levantar el triángulo equilátero pedido). Pero esta infinitud absoluta nos devolvería, en forma de caos, a la indeterminación de esa «recta delimitada» en el plano reglado por las rectas ilimitadas (de la prótasis). El diorismós establece la delimitación de ese conjunto infinito mediante otro conjunto infinito (porque, diríamos hoy, después de Cantor, «el todo es igual a la parte en los conjuntos infinitos») a saber, el conjunto de los infinitos radios pertenecientes a los círculos que tienen como centro los puntos A y B del segmento dado. |
c) Los versos 5 y 6 del soneto pueden considerarse como el diorismós de la propuesta en curso, desde el momento que amplían el espacio envolvente en que el autor locutor sitúa al manso (en relación a los dos mansos). Vemos que al manso reclamado le corresponde una esquila de estaño, mientras que al manso del mayoral extraño le corresponden collados (collares) de oro. Es decir, el mayoral del manso reclamado es más rico, el dueño que reclama es menos rico, pero no teme que las riquezas del mayoral extraño tengan fuerza bastante para apartarle de él. | |
| d) La kataskeué amplía el diorismós y lo organiza, disponiendo o preparando el contexto determinado como contexto determinante: dentro de este contexto habrá que seleccionar las rectas iguales a la dada, necesarias para formar el triángulo equilátero de la propuesta inicial. | d) Una vez delimitado el contexto (el campo) por el diorismós, cabe organizar o disponer los elementos definidos. «Como el manso cautivo que retienes va a venir a mí en cuanto lo liberes, yo te compensaré regalándote un toro blanco, virgen, que no tiene un año, que podrá ser tuyo por querencia surgida desde el principio». Se descarta que tú, mayoral extraño, puedas considerar «como tuyo en el alma» a mi manso, porque este vendrá a mí y tú te quedarías mutilado. Por ello te doy en albricias un blanco toro, como «regalo que acompaña a la buena nueva que te doy» al notificarte que el manso que tú reclamas no tiene querencia por tí, pero que todo puede arreglarse si aceptas mi toro añojo. |
|
| e) El curso del teorema entra en su tercera etapa, la etapa de su resolución. Etapa que comienza por la fase de la prueba o demostración. Tenemos ya organizados los términos del contexto determinante, y se trata ahora de probar que sus elementos determinan y concretan las relaciones entre los términos del sistema –por el hecho de formar parte de ese contexto– de un modo que nos aproximan al propósito inicial, que sigue actuando como idea directriz o telos del teorema. | e) El curso del poema entra en su tercera etapa, la de la resolución, una vez que ha sido organizado el contexto determinante. Es necesario probar, sin embargo, que los elementos que se han organizado o dispuesto en la kataskeué no son «meramente posibles», e indefinidos, sino determinados y determinantes de ciertas relaciones entre los términos del sistema. Hacen falta pruebas, sin duda. Pero si pides pruebas, si pides señas internas te las doy, te las detallo ahora mismo. |
|
| f) Finalmente, en el sympérasma, es cuando el telos propuesto en el principio del teorema, en su prótasis, puede ya ser identificado con la figura construida en la apódeixis. La prueba definitiva se encuentra en el mismo ajuste estético-idiográfico, singular, en la figura dibujada de las relaciones propuestas en abstracto en la prótesis; y este ajuste idiográfico-estético es sin embargo universal, porque es repetible indefinidamente en el espacio indefinido del plano. Quod Erat Faciendum. | f) Finalmente el autor o locutor puede decir al mayoral extraño que ese manso que tiene retenido, y cuya libertad pidió al principio, es el mismo que ahora ha sido identificado. Y como contraprueba (no ya del hecho, sino del conocimiento del hecho por parte del mayoral extraño) se le propondrá la prueba definitiva que justifica la demanda: «suelta mi manso» (vuelve a decirse ahora como en 1) y verásle como a mi choza viene libremente (con libertad-para). Lo que demostrará además y la vez que su dueño aún está vivo, que es el de antes, que tiene sal en las mismas manos que el manso va a lamer. Y este movimiento idiográficamente (estéticamente) atribuido «aureolarmente» al manso, será la prueba definitiva de mi propuesta que, aunque idiográfica, es universal, en la medida en que puede repetirse indefinidamente en el espacio indefinido constituido por las relaciones entre toros mansos, pastores y mayorales de las dehesas abstractas, ideales o imaginarias. Quod Erat Faciendum (o acaso, Q. E. D.). |